Projects
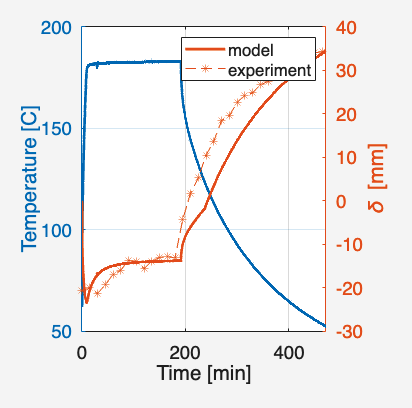
Bilamina Composite cure-induced deflection modeling
This MATLAB script models a composite laminate’s cure cycle by reading an experimental temperature profile, computing degree of cure, glass-transition temperature, evolving thermo-mechanical properties, thickness change, curvature, and final deflection, and compares the predicted deflection with experimental measurements.
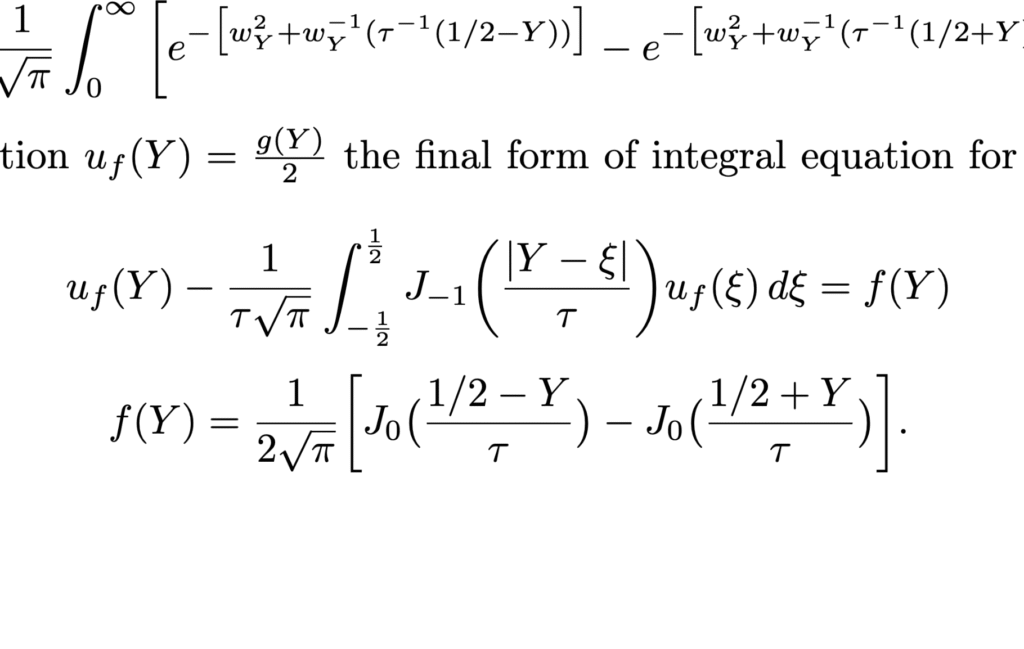
Couette Flow
Integral-Equation Solution of the Linearized BGK Model for Couette Flow
Starting from the linearized Boltzmann BGK model, I nondimensionalized the equations, simplified them for pure shear, applied boundary conditions, and solved analytically to obtain an integral equation that describes the Couette flow velocity field.
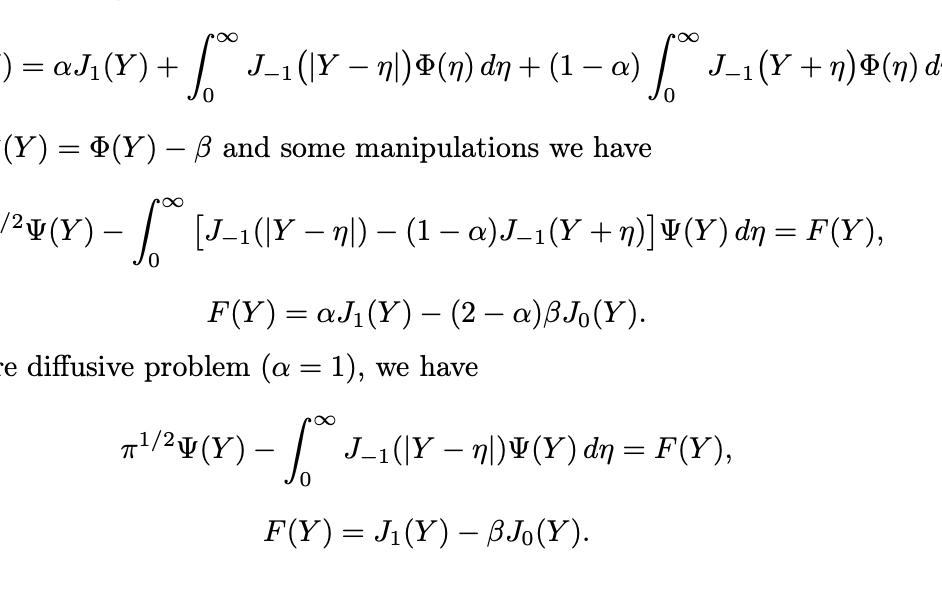
Kramers Flow
Integral-Equation Analysis of Kramers Flow Using the Linearized BGK Model
Starting with the linearized Boltzmann BGK equation, I modeled rarefied gas motion over a flat plate, applied slip-flow boundary conditions, derived and nondimensionalized the governing equations, and obtained an integral equation describing the velocity profile and its asymptotic behavior for Kramers flow.
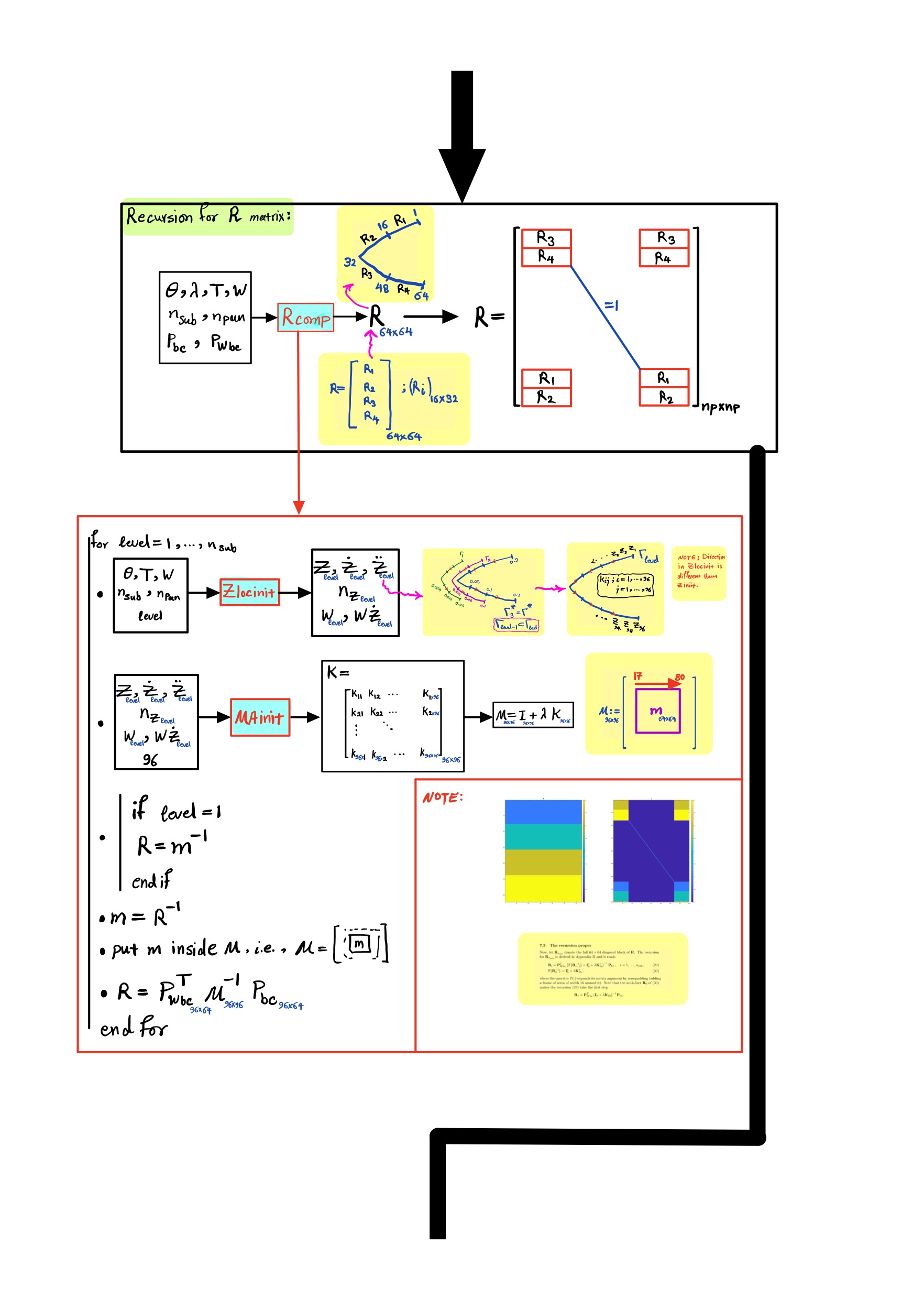
RCIP
RCIP for Cornered Integral Equations: Nyström Discretization, Compressed Inverse Recursion, and BGKW Kramers-Flow Application
I develop and explain the recursively compressed inverse preconditioning (RCIP) method for singular Fredholm integral equations with corner singularities—starting from where Neumann-series iterations fail, building a product Nyström discretization with complex-plane reformulation and Gauss–Legendre quadrature (including the diagonal curvature correction), constructing prolongation matrices and a coarse–fine compressed inverse via a level-wise recursion (with Schur–Banachiewicz speedup), and finally applying the scheme to the linearized BGKW Kramers-flow problem using Abramowitz functions J_n to obtain a stable, high-accuracy integral-equation solution.
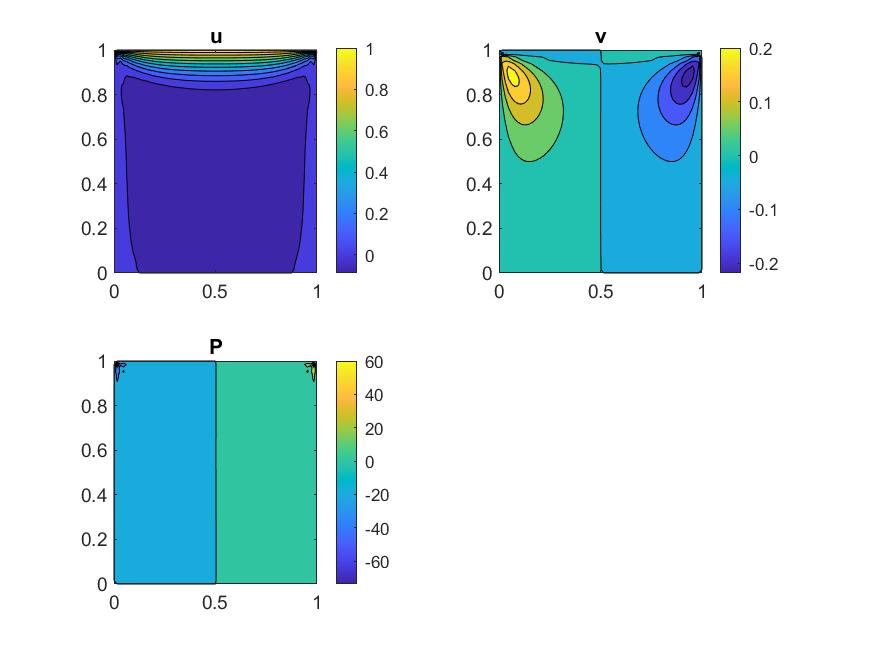
NS-MGM
Coupled-Pressure Navier–Stokes Solver with Multigrid Poisson Acceleration
This project implemented a benchmark lid-driven cavity flow simulation of the incompressible Navier–Stokes equations using a coupled pressure–velocity algorithm. The pressure field was obtained by solving the associated Poisson equation with a multigrid method, which dramatically accelerates convergence by efficiently removing both high- and low-frequency error components. Compared with a traditional single-grid approach, the multigrid-enhanced Poisson solver reduced iteration counts and overall run time while maintaining (and in many cases improving) solution accuracy. The result is a fast, stable, and highly accurate cavity-flow benchmark that highlights the advantages of combining a coupled pressure algorithm with multigrid acceleration for Navier–Stokes computations.
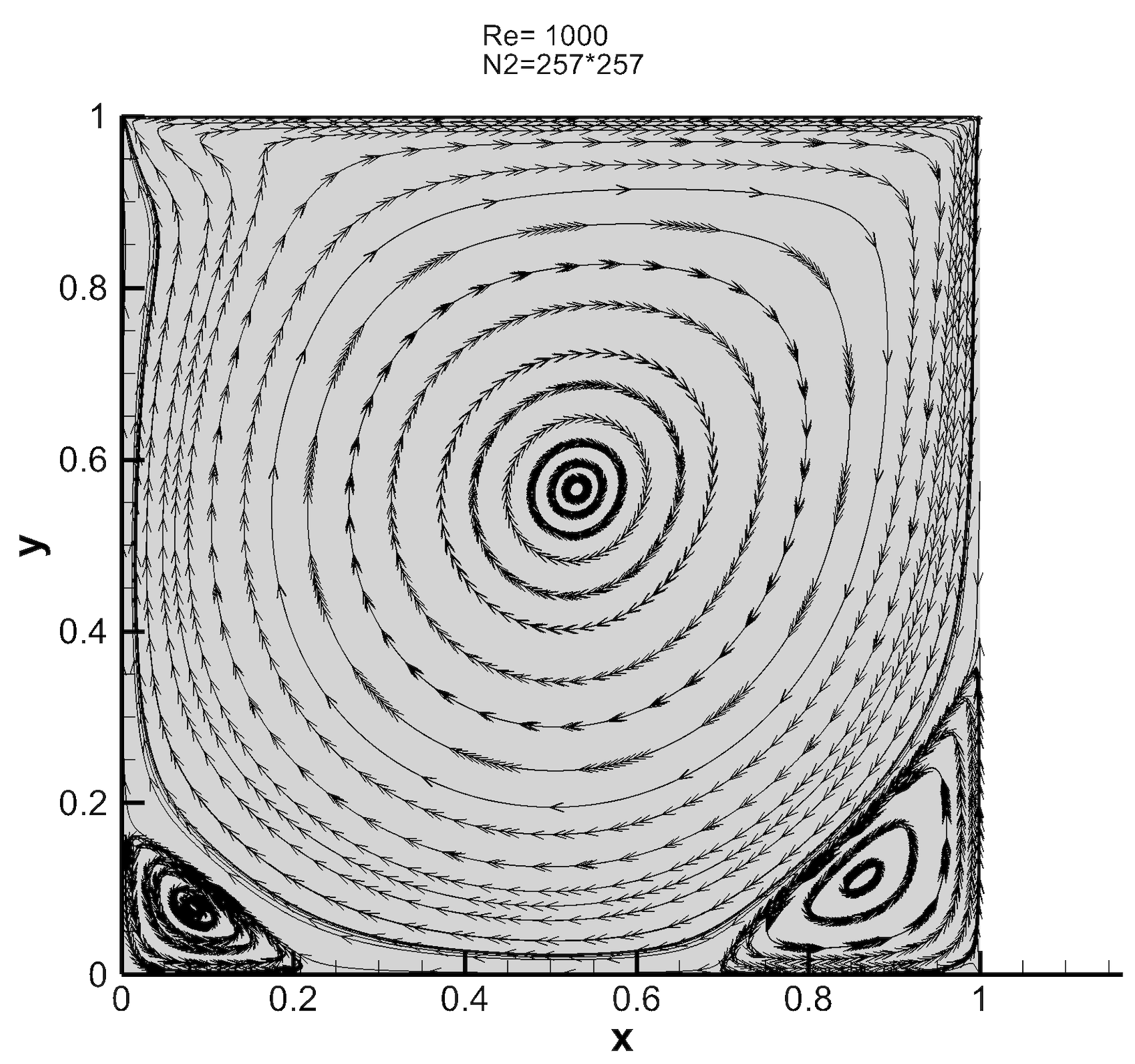
LBM-MRT-MGM
Lattice Boltzmann MRT Simulation of Lid-Driven Cavity Flow with Multigrid Poisson Pressure Solver
This project models the benchmark lid-driven cavity flow using the Lattice Boltzmann Method with Multiple-Relaxation-Time (LBM-MRT) for enhanced numerical stability and accuracy. To enforce incompressibility, a coupled pressure–velocity algorithm is employed in which the pressure Poisson equation is solved using a Multigrid Method (MGM). The multigrid approach efficiently removes both high- and low-frequency errors, dramatically speeding convergence and lowering computational cost while preserving accuracy. By combining LBM-MRT with an MGM-based pressure solver, the simulation achieves a fast, and precise solution for the cavity flow benchmark.

